PeterH Can you say it in simple words?
OK, go back to high school physics and geometric optics... notice all the nice straight lines forming similar triangles for a simple lens.
What happens there is that if you look at the star size (say HFD) as you go from intra-focus to focus, or extra focus to focus, you will see that the HFD from geometric optics form straight lines (with minimum HFD of zero).
As you get close to focus, diffraction starts to make the curve deviate from geometric optics. But further away from focus, where there are more points, the "curve" should take on a V shape (thus what autofocus is called).
However, in their infinite wisdom, ZWO assumes that it is a general 2nd order curve, ignoring Physics.
So they blindly use linear least squares (I guess that is what they learned in math, but not physics), and what you end up is the part of the conic section that is a parabola (what you usually see from ASIAIR).
Now, when I use a constrained 2nd order curve to model as a hyperbola, and thus get the straight sides of a V-curve.
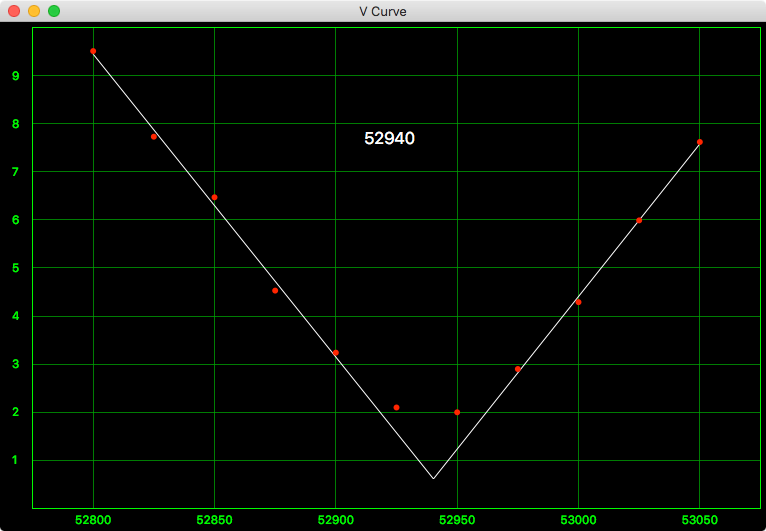
(I had use minimum mean square to solve, since it is easier to constrain the solutions to hyperbolas.)
Sorry, I can't make it simpler than this since it involves mathematics of conic sections. You either know it, or you don't know it. But look for the parabolas from ASIAIR, vs the V shaped curve above. I have a program that takes HFD for different eaf steps, and then spit out the focus EAF steps, if anyone is interested... Xcode project for macos.
Notice the very distinct point of the hyperbola (that is the estimated focus) instead of an indistinct rounded cusp. 52940 EAF steps, reported on the graph.
ZWO then makes another mistake of taking a second pass. They should not haven done that, but go straight to the minimum of the curve! Not only does it waste time, they are using singular data points and therefore has noisy data.
Two mistakes, compounding one another, and you end up with flakey autofocus in ASIAIR. When I use ASIAIR, I stop it after the first pass, look for the minimum, and go straight there. That way, there is only the inaccuracy of parabolas. On the second pass, you will notice that ASIAIR does not always end up at the parabola's minimum; and that causes big star blobs. Best is just to abandon ASIAIR and use something else, or Bahtinov masks.
Chen